-
-
Notifications
You must be signed in to change notification settings - Fork 39
Math FunctionFit
this package essentially consists of three objects:
- FunctionFit which estimates the parameters of a function, given some data.
- GeneralFunctionFit which does the same in a much slower way, but can deal with problems like local minima and such.
- AnotherGeneticOptimizer which finds minima of a function.
FunctionFit estimates the parameters of a function, given some data. it is a simple subclass of DhbLeastSquareFit, which uses Newton's method. as such it occasionally runs into problems, but when it has no problems, it is very fast. it has a simple interface: FunctionFit wants a function defined as a block and data as a collection of points, where point x is the independent var and point y the dependent one, iow data is a collection of points x@f(x). you can only have one (!) independent var and this var has to be at the first place in the value definition of the block (iow if you have several independent vars you have to put them into an Array or so and send them as one object to the function). everything, that follows the one independent var, is considered to be a parameter. lets make an example:
"the function:"
f:=[:independentVar :a :b|a*independentVar / (b+independentVar)].
"with 2 parameters it should be sufficient to have two datapoints:"
d:=#(2 10)collect: [:i|i@(f cull: i cull: 0.1 cull: 0.4) ]. "-->
{([email protected]). ([email protected])}"
"now we can define this:"
fit:= FunctionFit function: f data: d."-->
a FunctionFit for a SimpleParameterFunction( [:independentVar :a :b |
a * independentVar / (b + independentVar)] a: 0.937 b: 0.929) with
data of size: 2"
"you see that FunctionFit automatically initializes the parameters a and b.
you can change these startparameters with #parameters:. now we can calc the
fitting:"
fit evaluate ."-->
a SimpleParameterFunction( [:independentVar :a :b | a * independentVar /
(b + independentVar)] a: 0.09999999999999996 b: 0.39999999999999536)"
"you see that the fitting is not too exact."
fit precision . "-->5.402160287052362e-10"
"but then it was fast:"
fit iterations. "-->6"
"the precision btw is not the error of the fitting but the relative change
of the parameters. you can set the desired precision:"
fit desiredPrecision: 1.0e-13 .
"and simply rerun the evaluation:"
fit evaluate . "--> a SimpleParameterFunction( [:independentVar :a :b |
a * independentVar / (b + independentVar)] a: 0.09999999999999998 b: 0.39999999999999913)"
"that result is better. the initial desired precision is set relatively low
by the DHB package so that his iterative programs dont run into floating point
errors. defaultMaximumIterations is 50, which usually should be high enough,
but you can set it with #maximumIterations:. if you need the parameters for
further calculations, you get them this way:"
fit parameters. "--> #(0.09999999999999998 0.39999999999999913)"
"and you can evaluate the function itself with those parameters this way:"
fit value:2 . "--> 0.08333333333333334"
fit value:5 . "--> 0.09259259259259259"
fit value:10 ."--> 0.09615384615384615"
"if you compare that with the values of d - they are exactly the same
- you can see that a better result is not possible because of the floating
point errors "i guess thats it about the interface. i should mention that you can't set the function or the data separately for the object fit in this example. hence if you want to change eg the data or the function you have to make a new FunctionFit instance. now for the possible problems:
-
dont set the parameters to almost 0. you can set them for example to 0.0001 but if you set them to 0, an error will occur.
-
FunctionFit is essentially a hillclimber and as such it will run into every local minimum it finds. as an example we'll use this function:
f:=[ :x :a :b | (a * x) sin / (b + x squared) ].
d:=((-4) to: 4 by:0.1)collect: [:i|i@(f cull: i cull: 0.1 cull: 0.4) ].
fit:= FunctionFit function: f data: d.
fit evaluate . "-->
a SimpleParameterFunction( [ :x :a :b | (a * x) sin / (b + x squared) ]
a: 0.7808393474992235 b: 11.274634053262364)" "obviously wrong!"
"if you have an idea, what the parameters should be, you can set them accordingly:"
fit parameters:#(0.2 0.3). "-->a FunctionFit for a SimpleParameterFunction(
[ :x :a :b | (a * x) sin / (b + x squared) ] a: 0.2 b: 0.3) with data of size: 81"
fit evaluate . " a SimpleParameterFunction( [ :x :a :b | (a * x) sin /
(b + x squared) ] a: 0.1 b: 0.39999999999999997)" "now thats better!"
"but this can be difficult of course. then you could use GeneralFunctionFit,
wich should deal with this problem but is much slower."- another problem can appear when the algorithm runs into a singular error-matrix, in which case it cant find a solution. in this case GeneralFunctionFit should also find a solution, but, as i mentioned, its much slower. here is an example:
f:=[:x :a :b :alpha |(x/alpha) exp*a+b].
d:=((-4) to: 6 by:0.1)collect:
[:i|i@((f cull: i cull: 2 cull: 3 cull:3)*(Float random-0.5/4+1 )) ].
fit:= FunctionFit function: f data: d.
fit desiredPrecision: 1.0e-13 .
fit evaluate."-->
a SimpleParameterFunction( [ :x :a :b :alpha | (x / alpha) exp * a + b ]
a: 1.8057230765702041 b: 3.193436843975567 alpha: 2.814179700540481)"
"this obviously works, you won't expect the parameters to be exactly the same
with the multiplicative random error in the data. but with these data,
it doesn't work:"
billsData:={(0.0@2.109088219421704). (0.5@0.8814647496557722).
(1.0@0.3491858095389078). (1.5@0.20526532936509573).
(2.0@0.08850772880298544). (2.5@0.10098834478982013).
(3.0@0.1267192589527899). (3.5@0.15163580275973468).
(4.0@0.09161097555216349). (4.5@0.12967356857863194).
(5.0@0.07546349779080425). (5.5@0.08896841328836927).
(6.0@0.1307248042964248). (6.5@0.08526157258082188).
(7.0@0.11527453747811271). (7.5@0.09120326116648034).
(8.0@0.14292947664693562). (8.5@0.11193454959279178).
(9.0@0.0825855833015485). (9.5@0.11538774847974528).
(10.0@0.12170263580368511)}.
fit:= FunctionFit function: f data: billsData.
fit evaluate."--> SingularMatrixError:singular error matrix,
set better parameters"
"well ok, obviously time to have a look at GeneralFunctionFit"GeneralFunctionFit has essentially the same interface as FunctionFit, but it needs additionally a range for the parameters where it looks for a solution. this range is not a real constraint (constraint problems are for another package), it will also find solutions outside this range,as can be seen in the following example, but it is better if the probable solution is included in the range. you enter this range with an array of minimum values, or a single number for all parameters, and an array or a number for the maximum values for the parameters. let's have a look at the last example with billsData:
fit := GeneralFunctionFit function: f data: billsData minimumValues: 0
maximumValues: 5 . "--> a GeneralFunctionFit(AnotherGeneticOptimizer(
function: an ErrorOfParameterFunction( function: [:x :a :b :alpha |
(x / alpha) exp * a + b] relativeError: false errorType: #squared)
manager: AnotherChromosomeManager( popSize: 50 origin: #(0 0 0)
range: #(5 5 5) hammersley true MutRate: 0.4 CORate: 0.15 LCRate: 0.3
EIRRate: 0.15) maxIterations: 170 rangeScale: true removeLast: false
steadyState: true statistics: false result: nil))"
"unfortunately this problem is not the most simple one with 3 parameters,
hence i have to raise the populationsize"
fit populationSize: 500.
"this took 4 minutes:"
fit evaluate. "-->#(2.011261310866118 0.10509883594487042 -0.5018171309410887)"
"the minimum popsize for a good result in this case is 300 which takes 1 minute
on my computer, the popsize to use depends essentially on the number of parameters
to search for. the big popsize here was necessary because one parameter was outside
the range. if i adjust the range accordingly, things go faster:"
fit:=GeneralFunctionFit function: f data: billsData minimumValues: #(0 0 -1)
maximumValues: #(5 1 1) .
fit evaluate. "--> #(2.01126109846763 0.10509873942699106 -0.5018165817104505)"
"this returns the sqrt of the the mean squared error:"
fit error. "--> 0.025119657001123175"
"this is as good as it gets with the error in the data. if i remember correctly,
the real parameters before the random error was added, were: 2, 0.1, -0.5. you
can check the error of any parameter this way:"
fit error:#(2 0.1 -0.5). "-->0.02603738867204332"
"you get the parameters this way:"
fit function parameters. "-->
#(2.01126109846763 0.10509873942699106 -0.5018165817104505)"
"and you can calc the function values this way:"
fitted:=(0 to: 10 by:0.5)collect: [:i|i@(fit function value:i)].
lets take as another example the function that resulted in a local minimum:
"this is simple with only 2 parameters and should work without any problems"
f:=[ :x :a :b | (a * x) sin / (b + x squared) ].
d:=((-4) to: 4 by:0.1)collect: [:i|i@(f cull: i cull: 0.1 cull: 0.4) ].
fit := GeneralFunctionFit function: f data: d minimumValues: 0 maximumValues: 5 .
fit evaluate. "--> #(0.1 0.4)"GeneralFunctionFit can also do regressions with other error types. we'll use the last function f to explore these possibilities, since there are some interesting problems in this function (its not really simple to do a good fit). but first we'll add some error to the data d.
trueFunction:=((-4) to: 4 by:0.1)collect: [:i|i@(f cull: i cull: 0.1 cull: 0.4) ].
d:=((-4) to: 4 by:0.1)collect: [:i|(f cull: i cull: 0.1 cull: 0.4) ].
"now for the possibility of some outliers"
position:=((1 to: (d size))asArray shuffled copyFrom: 1 to: 8)."-->
#(51 77 47 19 67 69 40 43)"
cau:=DhbCauchyDistribution shape: 0 scale: 0.01.
position do: [:i|d at: i put:(( d at:i) + cau random)].
"and some normal randomness:"
normalD := DhbNormalDistribution new:1 sigma:0.2.
normalD1 := DhbNormalDistribution new:0 sigma:0.01.
mError:= ((-4) to: 4 by:0.1)with: d collect:
[:i :d|i@(d*normalD random+normalD1 random)].
"ok, we'll use that, it looks nice"
we can minimize the absolute error:
fit := GeneralFunctionFit function: f data: mError minimumValues: 0
maximumValues: 0.5.
"for comparison purposes we first calc the usual fit:"
fit evaluate ."--> #(0.08926526493766793 0.2498589951480392)"
squaredfit := ((-4) to: 4 by:0.1)collect: [:i|i@(fit function value:i)].
"now for the absolute error:"
fit errorType: #abs.
fit evaluate ." #(0.10084400745144963 0.4481057661350419)"
absfit := ((-4) to: 4 by:0.1)collect: [:i|i@(fit function value:i)].
"or the relative absolute error:"
fit relativeError: true.
"you can always look at the parameters and options by printing fit:"
fit. "--> a GeneralFunctionFit(AnotherGeneticOptimizer( function:
an ErrorOfParameterFunction( function: [:x :a :b | (a * x) sin /
(b + x squared)] relativeError: true errorType: #abs) manager:
AnotherChromosomeManager( popSize: 50 origin: #(0 0) range: #(0.5 0.5)
hammersley true MutRate: 0.4 CORate: 0.15 LCRate: 0.3 EIRRate: 0.15)
maxIterations: 170 rangeScale: true removeLast: false steadyState:
true statistics: false result: #(0.10084400745144963 0.4481057661350419)))"
fit evaluate ." #(0.09747788771529013 0.3771260237912653)"
absrelativefit := ((-4) to: 4 by:0.1)collect: [:i|i@(fit function value:i)].
or a zoom for better visibility, since the relative abs error optimization is very near to the true function in this case:

you can also use the median or quartile error that minimizes the radius of a tube around a percentage of the data:
fit relativeError: false.
fit errorType: #median."--> #quartile"
fit evaluate ." #(0.10027544739226098 0.48749006808189405)"
medianfit := ((-4) to: 4 by:0.1)collect: [:i|i@(fit function value:i)].
e:=fit error.
upper:=((-4) to: 4 by:0.1)collect: [:i|i@(e+(fit function value:i))].
lower:=((-4) to: 4 by:0.1)collect: [:i|i@((fit function value:i)-e)].
"let's check wether half of the datapoints are really inside the tube:"
inside :=0.
mError with: medianfit collect: [:t :a|((t y)-(a y))abs> e
ifFalse: [inside :=inside+1]ifTrue:[inside :=inside-1]].
inside."--> 1" "because mError size is odd"
Let's try different quartiles:
fit errorType: #quartile.
fit quartile: 0.3.
fit evaluate .
quartile3fit := ((-4) to: 4 by:0.1)collect: [:i|i@(fit function value:i)].
fit quartile: 0.5.
fit evaluate .
quartile5fit := ((-4) to: 4 by:0.1)collect: [:i|i@(fit function value:i)].
fit quartile: 0.7.
fit evaluate .
quartile7fit := ((-4) to: 4 by:0.1)collect: [:i|i@(fit function value:i)].
fit quartile: 0.9.
fit evaluate .
quartile9fit := ((-4) to: 4 by:0.1)collect: [:i|i@(fit function value:i)].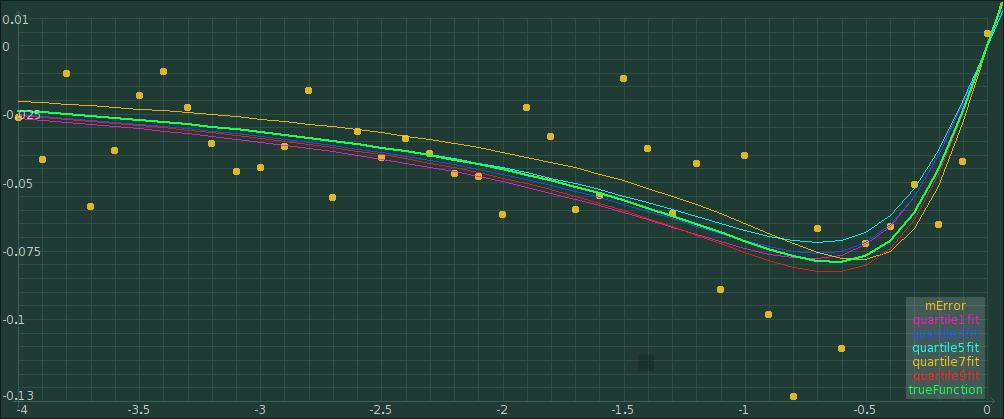
Of course with the quartile an additional parameter is introduced, which is somewhat problematic. therefore you have the method findQuartile, which repeatedly looks for the biggest bend (second derivative) in the sorted errors after throwing away eventually disturbing tails, iow it looks for a densely populated area that is most easily centered :
"first you have to set the errorType, as this works not only with #quartile"
fit errorType: #quartile.
fit findQuartile . "--> #(0.10339040298218138 0.43124900482018136)"
"and the used quartile:"
fit quartile. "--> (25/27)"
"now the result is actually not bad in this case, we store the function
data in a collection for later:"
quartile25d27 := ((-4) to: 4 by:0.1)collect: [:i|i@(fit function value:i)].
"but lets first have a short look how it works:"
ec:=fit errorCollection.
ec sort.
You see a clear bend at position 75, which corresponds to a quartile of 25/27=75/81. we can use this #findQuartile method to truncate the mError data correspondingly:
fit truncateData .
fit ."-->
a GeneralFunctionFit(AnotherGeneticOptimizer( function:
an ErrorOfParameterFunction( function: [:x :a :b | (a * x)
sin / (b + x squared)] relativeError: false errorType:
#quartile withQuartile: (25/27)) manager: AnotherChromosomeManager(
popSize: 100 origin: #(0 0) range: #(0.5 0.5) hammersley true
MutRate: 0.4 CORate: 0.15 LCRate: 0.3 EIRRate: 0.15) maxIterations:
170 rangeScale: true removeLast: false steadyState: true statistics:
false result: #(0.10339041020395343 0.43124906039580646))
data of size: 81truncated to: 75)"
"you can see here that the data is truncated to a size of 75,
corresponding to the quartile of 25/27. the datapoints with the 6
highest errors are temporarily thrown away. we now can calculate
eg a square fit or absolute fit with these data:"
fit errorType: #abs.
fit evaluate ."--> #(0.10084400765893727 0.4481057663541139)"
abstruncfit := ((-4) to: 4 by:0.1)collect: [:i|i@(fit function value:i)].
fit errorType: #squared.
fit evaluate ."--> #(0.0979902899696137 0.37835996060939986)"
"btw you can reset the data to its untruncated state :"
fit resetData. "-->
a GeneralFunctionFit(AnotherGeneticOptimizer( function: an
ErrorOfParameterFunction( function: [:x :a :b | (a * x) sin /
(b + x squared)] relativeError: false errorType: #squared)
manager: AnotherChromosomeManager( popSize: 100 origin: #(0 0)
range: #(0.5 0.5) hammersley true MutRate: 0.4 CORate: 0.15
LCRate: 0.3 EIRRate: 0.15) maxIterations: 170 rangeScale: true
removeLast: false steadyState: true statistics: false result:
#(0.0979902899696137 0.37835996060939986)) data of size: 81)"and the truncated results are not bad:

well, i guess thats essentially it about generalFunctionFit. there are a few other settable parameters and another errortype #insensitive that is similar to quartile, it calcs a theoretical tube radius as error and tries to center the tube within the errors outside of the tube, but thats nothing important - i made it before i made #findQuartile, which in a way does the same thing in a cleaner way.
AnotherGeneticOptimizer finds minima of a function. DHB already has a DhbGeneticOptimizer, but its not too efficient, hence i subclassed one that is better tuned to the problem. it can be used the same way as DhbGeneticOptimizer. but it can also be used similarly to GeneralFunctionFit with AnotherGeneticOptimizer function: f minimumValues: anArray maximumValues: anotherArray. f has to be a block with only one variable, and that variable has to always be an Array. as a simple example we'll use De Jongs first function, which is just the square of a vector and has a minimum if every element of the vector is zero:
f:=[:x| |v| v:=x asDhbVector . v*v].
"simple F1 dejong"
origin:= #(-5 -5 -5 -5).
range:=#(10 10 10 10).
optimizer:= AnotherGeneticOptimizer function: f minimumValues:
origin maximumValues: origin negated. "-->
AnotherGeneticOptimizer( function: [:x |
| v |
v := x asDhbVector.
v * v] manager: AnotherChromosomeManager( popSize: 50 origin:
#(-5 -5 -5 -5) range: #(10 10 10 10) hammersley true MutRate: 0.4
CORate: 0.15 LCRate: 0.3 EIRRate: 0.15) maxIterations: 170 rangeScale:
true removeLast: false steadyState: true statistics: false result: nil)"
[guess:= optimizer evaluate]timeToRun . "--> 1800"
guess. "-->
#(1.023543377486446e-9 5.198641820526351e-9
4.508047806965468e-10 -6.540242549503236e-9)"
"you can see that the populationsize is 50 and the maximum number
of iterations 170. now this optimizer is much slower then
DhbGeneticOptimizer, hence to make a fair comparison with
DhbGeneticOptimizer i have to raise both values:"
optimizer2:= DhbGeneticOptimizer minimizingFunction: f.
optimizer2 maximumIterations:1000.
manager2:= DhbVectorChromosomeManager new:100 mutation: 0.1 crossover: 0.4.
manager2 origin: origin; range: range.
optimizer2 chromosomeManager: manager2.
[guess2:= optimizer2 evaluate]timeToRun . "-->1824"
guess2. "-->
a DhbVector(0.00034134762803716967 -0.0020883758742629155
-0.0010854728135312186 0.0005708957092682709)"
"lets try de jongs second function, Rosenbrock’s valley, which is a bit
more difficult (we do just 2 dimensions), minimum is at 1:"
f:=[:x| (x overlappingPairsCollect: [:f :s|
(s - f squared)squared *100 + (1-f)squared])sum ].
origin:= #(-2.048 -2.048 ).
range:=#( 4.096 4.096 ).
optimizer:= AnotherGeneticOptimizer function: f minimumValues: origin
maximumValues: origin negated.
[guess:= optimizer evaluate]timeToRun ."--> 852"
guess."--> #(0.9999997383264783 0.9999994594233975)"
optimizer2:= DhbGeneticOptimizer minimizingFunction: f.
optimizer2 maximumIterations:1000.
manager2:= DhbVectorChromosomeManager new:100 mutation: 0.1 crossover: 0.4.
manager2 origin: origin; range: range.
optimizer2 chromosomeManager: manager2.
[guess2:= optimizer2 evaluate]timeToRun . "--> 2008"
guess2. "--> a DhbVector(0.9799938028063941 0.960796344947942)"
"de jongs third function is a step function where the range is originally
constrained. i use an unconstrained version:"
f:=[:x| (x floor + 0.5)squared sum ].
origin:= #(-5 -5 ).
range:=#( 10 10 ).
optimizer.
optimizer:= AnotherGeneticOptimizer function: f minimumValues:
origin maximumValues: origin negated.
[guess:= optimizer evaluate]timeToRun ." 3572"
guess." #(-0.45063687066974 0.24941200602086866)"
f value: guess. "-->0.5" "iow it is the global minimum"
optimizer2:= DhbGeneticOptimizer minimizingFunction: f.
optimizer2 maximumIterations:1000.
manager2:= DhbVectorChromosomeManager new:100 mutation: 0.1 crossover: 0.4.
manager2 origin: origin; range: range.
optimizer2 chromosomeManager: manager2.
[guess2:= optimizer2 evaluate]timeToRun . "-->113024"
guess2. "--> a DhbVector(-4.871008072539096 0.6201139908272513)"
f value: guess2. "-->1148422292309540889"
"well, i feared that AnotherGeneticOptimizer finds the minimum by chance
and enlarged the search range to origin:= #(-50 -50 ) and kept the small
popsize, but it found the minimum nevertheless."
"de jongs fourths function has some strong randomness in it, minimum is at 0:"
normalD := DhbNormalDistribution new:0 sigma:1.
f:=[:x|(x withIndexCollect: [:a :i|i*(a raisedToInteger: 4)])sum + normalD random].
origin:= #(-1.28 -1.28 ).
range:=#( 2.56 2.56 ).
optimizer:= AnotherGeneticOptimizer function: f minimumValues: origin
maximumValues: origin negated.
[guess:= optimizer evaluate]timeToRun . "-->326"
guess."--> #(0.33423054346990877 0.035405028798253566)"
optimizer2:= DhbGeneticOptimizer minimizingFunction: f.
optimizer2 maximumIterations:1000.
manager2:= DhbVectorChromosomeManager new:100 mutation: 0.1 crossover: 0.4.
manager2 origin: origin; range: range.
optimizer2 chromosomeManager: manager2.
[guess2:= optimizer2 evaluate]timeToRun ."--> 2450"
guess2. "-->a DhbVector(0.28986057396120546 -0.41531812926628564)"
"with repeated evaluations this is definitively a draw. but then
the randomness seems a bit high for general optimizers like this.
i guess, i'd construct (that wouldnt be too complicated) and use
a more specialised genetic algo for this kind of problem (those
things usually arise in real-time problems, where one would use
a more specialised solution)."
"de jongs fifth function, Shekel's foxholes, the minimum is at -32:"
f:=[:x| |x1 x2| x1:=x at:1. x2:=x at:2. 1/(( (-2 to:2) collect:
[:i| ((-2 to:2) collect:[:j| 1/( 5*(i+2) + j +3 +
((x1 - (16 * j) )raisedToInteger: 6 ) +
((x2 - (16 * i) )raisedToInteger: 6 ) ) ])sum])sum + 0.002)].
origin:= #(-65.536 -65.536 ).
range:=#( 131.072 131.072 ).
optimizer:= AnotherGeneticOptimizer function: f minimumValues:
origin maximumValues: origin negated.
[guess:= optimizer evaluate]timeToRun . "--> 2258"
guess." #(-31.978334268258692 -31.97833052152327)"
"doesnt look too good, but:"
f value: #(-32 -32)." 0.998003838818649"
f value:guess. " 0.9980038377944489"
"the guess is better. i suppose there are some floating point errors
in my naive implementation of the 5th de jong function."
optimizer2:= DhbGeneticOptimizer minimizingFunction: f.
optimizer2 maximumIterations:1000.
manager2:= DhbVectorChromosomeManager new:100 mutation: 0.1 crossover: 0.4.
manager2 origin: origin; range: range.
optimizer2 chromosomeManager: manager2.
[guess2:= optimizer2 evaluate]timeToRun ."--> 12994"
guess2. "-->a DhbVector(-31.97683084371497 -31.992919975408093)"
"the first guess was better:"
f value: #(-32 -32)." 0.998003838818649"
f value:guess2. " 0.9980038381147325"
f value:guess. " 0.9980038377944489"
"Griewank's function is somewhat difficult, the minimum is at 0:"
g:=[:x| x squared sum / 4000- ((x withIndexCollect:
[ :xi :i| (xi / i sqrt)cos]) reduce:[:a :b|a*b]) + 1].
origin:= #(-600 -600 ).
range:=#( 600 600 ).
optimizer:= AnotherGeneticOptimizer function: g minimumValues:
origin maximumValues: range.
optimizer evaluate. "-->#(4.9758079672135535e-9 -2.4189195162844996e-9)"
g value: optimizer result. "-->0.0"
"but if you repeat that , occasionally you get a wrong result,
at least with the standard popsize and maximumIterations.
iow here we are at the frontier of what the algorithm can do,
if you want to compare it to other algos."
optimizer2:= DhbGeneticOptimizer minimizingFunction: g.
optimizer2 maximumIterations:1000.
manager2:= DhbVectorChromosomeManager new:100 mutation: 0.1 crossover: 0.4.
manager2 origin: origin; range: range.
optimizer2 chromosomeManager: manager2.
optimizer2 evaluate. "-->a DhbVector(-6.463181701024041 -0.17632856451621137)"
"this problem is a bit too difficult for the original minimizer"
"now for some serious problem, the damavandi test function:"
f:=[:x| |x1 x2| x1:=x at:1. x2:=x at:2.( 1 - ( ( ((x1 - 2)* Float pi)sin *
((x2 - 2) * Float pi)sin /(Float pi squared *(x1 - 2)*(x2 - 2)) )abs
raisedToInteger: 5)) *(2 + (x1 - 7) squared + (2 * (x2 -7)squared)) ].
origin:= #(0 0 ).
range:=#( 14 14 ).
"i had to raise the populationsize considerably to solve this
(iow it is indeed difficult for a 2-dimensional problem):"
optimizer:= AnotherGeneticOptimizer function: f minimumValues:
origin maximumValues: range.
optimizer chromosomeManager populationSize: 570.
[optimizer evaluate]timeToRun ."--> 0:00:03:23.145"
optimizer result."--> #(1.9999999765914496 1.999999985173217)"
f value:optimizer result."--> 5.556666276540919e-13"
"theoretically the minimum is 0 at values of 2,
hence that result is ok. with a repeated evaluation the
f value:optimizer result would of course come down to 0"
"and finally for a really difficult 5-dimensional problem:
the DeVilliers-Glasser 2 function"
ti:=[:x| x -1* 0.1 ] .
yi:=[:i| 53.81 * (1.27 raisedTo: (ti value: i)) * (3.012 *
(ti value: i)+ (2.13 *(ti value: i) )sin ) tanh *
(0.507 exp * (ti value: i))cos].
f :=[:x| |xc| xc:=x collect: [:i|i<0 ifTrue: [i negated ] ifFalse: [i]].
( (1 to: 24)collect: [:i|
(((xc at:2)raisedTo: (ti value: i))* (xc at:1)*( (xc at:3)*
(ti value: i) + ((xc at:4)*(ti value: i))sin )tanh *
( (xc at:5)exp *(ti value: i))cos - (yi value: i))squared ])sum ].
":this is a box-bounded problem, hence i simply mapped negative values
onto its positive ones."
origin:= #(0 0 0 0 0).
range:= #(60 60 60 60 60).
optimizer:= AnotherGeneticOptimizer function: f minimumValues: origin
maximumValues: range .
"because this problem has 5 dimensions we need a higher populationSize:"
optimizer chromosomeManager populationSize: 600.
optimizer maximumIterations: 200.
[guess:= optimizer evaluate]timeToRun ." 0:00:05:34.788"
guess abs."-->
#(53.8072320801814 1.270035998256502 3.0159350950400166
2.1259190198599427 0.5070196896821256)"
f value:guess ." 7.164439709136837e-5"
"the minimum is at 0 with x = #(53.81, 1.27, 3.012, 2.13, 0.507).
but with repeated evaluations it often gets stuck in local minima.
iow the algo definitively has serious problems with this function.
eg i usually get a result like this:
guess abs. #(53.80999863690706 1.2700000173122075 3.012001866954813
64.96185121607915 4.113682216435432)
f value:guess . 5.498009373365465e-13
well, usually the literature says (and the authors use that fact in their
testing) that the x values are restricted to be <60, only once i read <500."i should mention that the genetic operators used in this implementation are simply those used by H. Mühlenbein in his breeder genetic algorithm, and its easy to find many papers about this in the internet.